语音识别时,人说一句“Hello”,尽管发音很标准,但是由于有停顿、换气或是其他原因,音频信息中的“H”音很容易对不上文本信息中的“H”。这就需要预处理对齐问题,但是用人工的方法手动对齐比较音频信息和文本信息,需要耗费大量的人力财力。CTC就是处理这一类对齐问题而生的技术。
基本过程
在语音识别中,CTC会逐帧辨别发的什么音。如果通过发音辨别出了一个字母,那么这一帧就标记为这个字母;如果没声音就标记为blank,表示这是两个单词中间的空格;如果分辨不出来是啥,就标记为ϵ (ctc blank)。所以将“Hello”的音频信息进行辨别后,会得到的结果可能会是:“ϵϵHellϵϵlloϵ”,也可能是“Heeϵϵllϵϵlooϵϵ”,还有其他很多种可能。
ctc的处理过程分为2步:
- 将识别结果中相邻的重复字符删掉,那么“ϵϵHellϵϵlloϵ”就变成了“ϵHelϵloϵ”,“Heeϵϵllϵϵlooϵϵ”就变成了“Heϵlϵloϵ”;
- 删去ϵ,“ϵHelϵloϵ”和“Heϵlϵloϵ”就都变成了“Hello”。
我们的目的是求出P(lable|x),其中x是输入的数据,lable是标签数据,即正确的输出。P(lable|x)表示的是,如果在输入数据为x的条件下,能够正确输出标签数据的概率有多大,这个概率肯定是越大越好,如果P(lable|x)=1,那么就说明百分之百可以正确输出。
Loss的定义如下,如果P(lable|x)越接近1,Loss就接近于0;如果P(lable|x)越接近0,Loss就会越大:
$$
Loss=-\ln P(lable|x)
$$
P(lable|x)如何计算呢?从上面ctc的处理过程可以看出来,有很多种序列最终都可以处理为标签数据,“ϵϵHellϵϵlloϵ”就是一条可以被处理为“Hello”的序列,记其为seq,那么产生seq的概率有多少呢?这里$y_c^t$表示在第t时间步生成字符c的概率有多少,那么要生成seq这么长的序列,就要把生成每个字符的概率乘起来。
$$
P(seq|x)=y_\epsilon^1 \times y_\epsilon^2 \times y_H^3 \times y_e^4 \times y_l^5 \times y_l^6 \times y_\epsilon^7 \times y_\epsilon^8 \times y_l^9 \times y_l^{10} \times y_o^{11} \times y_\epsilon^{12}
$$
如果再用π来表示一个序列的集合,这个集合中所有的序列和seq一样,经过ctc处理过后,都可以变为标签数据。那么将这个集合中所有序列的概率加起来,就是P(lable|x)。
$$
P(lable|x)=\sum_{\pi}P(\pi|x)
$$
可是,π集合中有多少序列呢,茫茫多的序列都可以转为lable。如果lable是“cat”的话,那么可以转为“cat”的序列数,可以通过下图可以看出来,白色节点表示识别为字母,黑色节点表示识别不出来是个啥,标记为“ϵ”(图片来自网络):
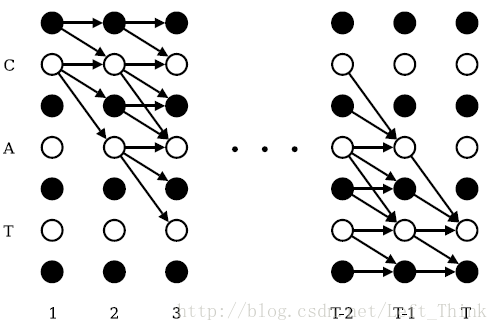
每一条路径都是一种语音识别的结果,而且此结果可以经由ctc处理后转换为标签数据。这才3个字母,就这么条路径,如果成百上千的单词,一一计算每种可能的话,这个计算量很大。
使用动态规划优化
动态规划的思想是自顶向下写一个递归式,然后自底向上算出来。
如上文所述,在t个时间步走到字符“u”的路线有很多条,如果seq是其中一条路线,那么其概率为:
$$ P(seq|x)=\prod_{i=1}^{t} y^i_{{seq}_i} $$这里定义一个函数α(t,u),表示在t个时间步走到字符“u”的概率。用π表示所有可以在t个时间步走到字符“u”的路线集合,那么有:
$$ \alpha(t,u)=\sum_{\pi}\prod_{i=1}^{t} y^i_{\pi_i} $$再看看刚刚开始那个例子“Hello”,如果当前在第t个时间步,判别成了一个字符“l”,那么在第t-1个时间步上,可以是哪些字符呢?
这要分2种情况讨论:
第一种情况
如果“Hello”的第一个“l”,也就是”Hello”标红的那个“l”,那么在第t-1个时间步上,可以是“e”、“ϵ”、“l”三种情况;
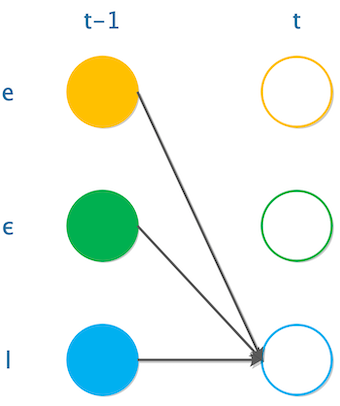
所以要求第t个时间步走到“l”的概率,就要先求出在t-1个时间步走到“e”、“ϵ”、“l”的概率,求和之后,再乘以$y_c^t$,即:
$$
\alpha(t,u)=y_u^t[\alpha(t-1,u)+\alpha(t-1,u-1)+\alpha(t-1,u-2)]
$$
这里u-1和u-2表示字符u的上一个字符和上两个字符。
第二种情况
如果是“Hello”的第二个“l”,也就是“Hello”标红的那个“l”,那么在第t-1个时间步上,只可以是“ϵ”、“l”两种情况。要是算上上面的“l”,那么这两个“l”会合并成1个;如果是在t个时间步上走到了“ϵ”这个字符,那么在t-1个时间步上,也只能是“l”、“ϵ”两种情况。要是也算上上面一个“ϵ”,那么会跨过中间这个“l”,这个字符就不输出了。
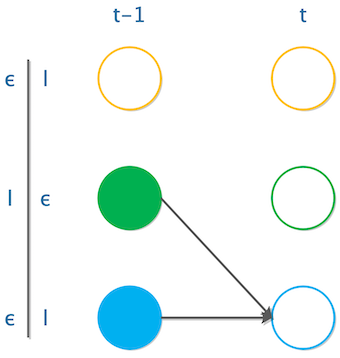
所以第t个时间步走到“l”或”ϵ“,只能横着走过来,或从上一个字符过来,概率即:
$$
\alpha(t,u)=y_u^t[\alpha(t-1,u)+\alpha(t-1,u-1)]
$$
这样递归公式就定义好了,再算一下递归式子的底:
$$
\alpha(1,1)=y_\epsilon^1
$$
$$
\alpha(1,2)=y_h^1
$$
$$
\alpha(1,u)=0 \quad u>2
$$
从这个底开始,使用递推公式自底向上的计算,直至算出$\alpha(T,lable)+\alpha(T,lable-1)$,T表示总时间步,所有可以经过ctc转化为“Hello”的序列,最后一个字符可以是“ϵ”也可以是“o”。label表示所最后一个字符是“ϵ”,label-1表示最后一个字符是“o”,这样走出的路线都可以经过ctc转化为“Hello”。